![]() 江苏省苏州、无锡、常州、镇江四市2017-2018学年度高三3月调研考试数学试题.doc
江苏省苏州、无锡、常州、镇江四市2017-2018学年度高三3月调研考试数学试题.doc
一、填空题:本大题共14个小题,每小题5分,共70分.请把答案填写在答题卡相应位置上.
1.已知集合![]() ,
,![]() ,则集合
,则集合![]() .
.
2.已知复数![]() 满足
满足![]() (
(![]() 为虚数单位),则
为虚数单位),则![]() .
.
3.双曲线![]() 的渐近线方程为 .
的渐近线方程为 .
4.某中学共有![]() 人,其中高二年级的人数为
人,其中高二年级的人数为![]() .现用分层抽样的方法在全校抽取
.现用分层抽样的方法在全校抽取![]() 人,其中高二年级被抽取的人数为
人,其中高二年级被抽取的人数为![]() ,则
,则![]() .
.
5.将一颗质地均匀的正四面体骰子(每个面上分别写有数字![]() ,
,![]() ,
,![]() ,
,![]() )先后抛掷
)先后抛掷![]() 次,观察其朝下一面的数字,则两次数字之和等于
次,观察其朝下一面的数字,则两次数字之和等于![]() 的概率为 .
的概率为 .
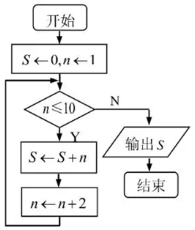
6.如图是一个算法的流程图,则输出![]() 的值是 .
的值是 .
7.若正四棱锥的底面边长为![]() ,侧面积为
,侧面积为![]() ,则它的体积为
,则它的体积为 ![]() .
.
8.设![]() 是等差数列
是等差数列![]() 的前
的前![]() 项和,若
项和,若![]() ,
,![]() ,则
,则![]() .
.
9.已知![]() ,
,![]() ,且
,且![]() ,则
,则![]() 的最小值是 .
的最小值是 .
10.设三角形![]() 的内角
的内角![]() ,
,![]() ,
,![]() 的对边分别为
的对边分别为![]() ,
,![]() ,
,![]() ,已知
,已知![]() ,则
,则![]() .
.
11.已知函数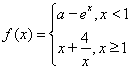 (
(![]() 是自然对数的底).若函数
是自然对数的底).若函数![]() 的最小值是
的最小值是![]() ,则实数
,则实数![]() 的取值范围为 .
的取值范围为 .
12.在![]() 中,点
中,点![]() 是边
是边![]() 的中点,已知
的中点,已知![]() ,
,![]() ,
,![]() ,则
,则![]() .
.
13.已知直线![]() :
:![]() 与
与![]() 轴交于点
轴交于点![]() ,点
,点![]() 在直线
在直线![]() 上,圆
上,圆![]() :
:![]()
上有且仅有一个点![]() 满足
满足![]() ,则点
,则点![]() 的横坐标的取值集合为 .
的横坐标的取值集合为 .
14.若二次函数![]()
![]() 在区间
在区间![]() 上有两个不同的零点,则
上有两个不同的零点,则![]() 的取值范围为 .
的取值范围为 .
二、解答题:本大题共6小题,共计90分.请在答题卡指定区域内作答,解答应写出文字说明、证明过程或演算步骤.
15.已知向量![]() ,
,![]() .
.
(1)若角![]() 的终边过点
的终边过点![]() ,求
,求![]() 的值;
的值;
(2)若![]() ,求锐角
,求锐角![]() 的大小.
的大小.
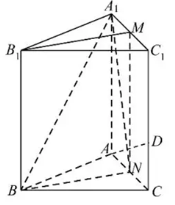
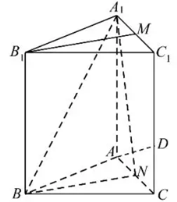 16.如图,正三棱柱
16.如图,正三棱柱![]() 的高为
的高为![]() ,其底面边长为
,其底面边长为![]() .已知点
.已知点![]() ,
,![]() 分别是棱
分别是棱![]() ,
,![]() 的中点,点
的中点,点![]() 是棱
是棱![]() 上靠近
上靠近![]() 的三等分点.
的三等分点.
求证:(1)![]() 平面
平面![]() ;
;
(2)![]() 平面
平面![]() .
.
17.已知椭圆![]() :
:![]()
![]() 经过点
经过点![]() ,
,![]() ,点
,点![]() 是椭圆的下顶点.
是椭圆的下顶点.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)过点![]() 且互相垂直的两直线
且互相垂直的两直线![]() ,
,![]() 与直线
与直线![]() 分别相交于
分别相交于![]() ,
,![]() 两点,已知
两点,已知![]() ,求直线
,求直线![]() 的斜率.
的斜率.
18.如图,某景区内有一半圆形花圃,其直径![]() 为
为![]() ,
,![]() 是圆心,且
是圆心,且![]() .在
.在![]() 上有一座观赏亭
上有一座观赏亭![]() ,其中
,其中![]() .计划在
.计划在![]() 上再建一座观赏亭
上再建一座观赏亭![]() ,记
,记![]() .
.
(1)当![]() 时,求
时,求![]() 的大小;
的大小;
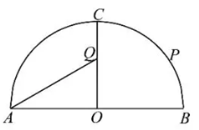 (2)当
(2)当![]() 越大,游客在观赏亭
越大,游客在观赏亭![]() 处的观赏效果越佳,求游客在观赏亭
处的观赏效果越佳,求游客在观赏亭![]() 处的观赏效果最佳时,角
处的观赏效果最佳时,角![]() 的正弦值.
的正弦值.
19.已知函数![]() ,
,![]() .
.
(1)若![]() ,
,![]() ,且
,且![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(2)若![]() ,且函数
,且函数![]() 在区间
在区间![]() 上是单调递减函数.
上是单调递减函数.
①求实数![]() 的值;
的值;
②当![]() 时,求函数
时,求函数![]() 的值域.
的值域.
20.已知![]() 是数列
是数列![]() 的前
的前![]() 项和,
项和,![]() ,且
,且![]()
![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)对于正整数![]() ,
,![]() ,
,![]() ,已知
,已知![]() ,
,![]() ,
,![]() 成等差数列,求正整数
成等差数列,求正整数![]() ,
,![]() 的值;
的值;
(3)设数列![]() 前
前![]() 项和是
项和是![]() ,且满足:对任意的正整数
,且满足:对任意的正整数![]() ,都有等式
,都有等式![]()
![]()
![]() 成立.求满足等式
成立.求满足等式![]() 的所有正整数
的所有正整数![]() .
.
2017-2018学年度苏锡常镇四市高三教学情况调研(一)
数学Ⅱ(附加题)
21.【选做题】在A,B,C,D四小题中只能选做两题,每小题10分,共计20分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.
B. 选修4-2:矩阵与变换
已知矩阵![]() ,
,![]() ,列向量
,列向量![]() .
.
(1)求矩阵![]() ;
;
(2)若![]() ,求
,求![]() ,
,![]() 的值.
的值.
C. 选修4-4:坐标系与参数方程
在极坐标系中,已知圆![]() 经过点
经过点![]() ,圆心为直线
,圆心为直线![]() 与极轴的交点,求圆
与极轴的交点,求圆![]() 的极坐标方程.
的极坐标方程.
【必做题】第22题、第23题,每题10分,共计20分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.
22.如图,在四棱锥![]() 中,底面
中,底面![]() 是矩形,
是矩形,![]() 垂直于底面
垂直于底面![]() ,
,![]() ,点
,点![]() 为线段
为线段![]() (不含端点)上一点.
(不含端点)上一点.
(1)当![]() 是线段
是线段![]() 的中点时,求
的中点时,求![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
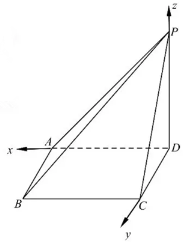 (2)已知二面角
(2)已知二面角![]() 的正弦值为
的正弦值为![]() ,求
,求![]() 的值.
的值.
23.在含有![]() 个元素的集合
个元素的集合![]() 中,若这
中,若这![]() 个元素的一个排列(
个元素的一个排列(![]() ,
,![]() ,…,
,…,![]() )满足
)满足![]() ,则称这个排列为集合
,则称这个排列为集合![]() 的一个错位排列(例如:对于集合
的一个错位排列(例如:对于集合![]() ,排列
,排列![]() 是
是![]() 的一个错位排列;排列
的一个错位排列;排列![]() 不是
不是![]() 的一个错位排列).记集合
的一个错位排列).记集合![]() 的所有错位排列的个数为
的所有错位排列的个数为![]() .
.
(1)直接写出![]() ,
,![]() ,
,![]() ,
,![]() 的值;
的值;
(2)当![]() 时,试用
时,试用![]() ,
,![]() 表示
表示![]() ,并说明理由;
,并说明理由;
(3)试用数学归纳法证明:![]() 为奇数.
为奇数.
2017-2018学年度苏锡常镇四市高三教学情况调研(一)
数学Ⅰ试题参考答案
一、填空题
1. ![]() 2.
2. ![]() 3.
3. ![]() 4.
4. ![]() 5.
5. ![]()
6. ![]() 7.
7. ![]() 8.
8. ![]() 9.
9. ![]() 10.
10. ![]()
11. ![]() 12.
12. ![]() 13.
13. ![]() 14.
14. ![]()
二、解答题
15.解:(1)由题意![]() ,
,![]() ,
,
所以![]()
![]()
![]()
![]()
![]() .
.
(2)因为![]() ,所以
,所以![]() ,即
,即![]()
![]() ,所以
,所以![]() ,
,
则![]()
![]() ,对锐角
,对锐角![]() 有
有![]() ,所以
,所以![]() ,
,
所以锐角![]() .
.
16.证明:(1)连结![]() ,正三棱柱
,正三棱柱![]() 中,
中,![]() 且
且![]() ,则四边形
,则四边形![]() 是平行四边形,因为点
是平行四边形,因为点![]() 、
、![]() 分别是棱
分别是棱![]() ,
,![]() 的中点,所以
的中点,所以![]() 且
且![]() ,
,
又正三棱柱![]() 中
中![]() 且
且![]() ,所以
,所以![]() 且
且![]() ,所以四边形
,所以四边形![]() 是平行四边形,所以
是平行四边形,所以![]() ,又
,又![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ;
;
(2)正三棱柱![]() 中,
中,![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,所以
,所以![]() ,
,
正![]() 中,
中,![]() 是
是![]() 的中点,所以
的中点,所以![]() ,又
,又![]() 、
、![]() 平面
平面![]() ,
,![]() ,
,
所以![]() 平面
平面![]() ,又
,又![]() 平面
平面![]() ,
,
所以![]() ,
,
由题意,![]() ,
,![]() ,
,![]() ,
,![]() ,所以
,所以![]() ,
,
又![]() ,所以
,所以![]() 与
与![]() 相似,则
相似,则![]() ,
,
所以![]()
![]() ,
,
则![]() ,又
,又![]() ,
,![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
17.解:(1)由题意得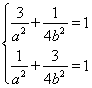 ,解得
,解得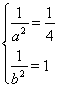 ,
,
所以椭圆![]() 的标准方程为
的标准方程为![]() ;
;
(2)由题意知![]() ,直线
,直线![]() ,
,![]() 的斜率存在且不为零,
的斜率存在且不为零,
设直线![]() :
:![]() ,与直线
,与直线![]() 联立方程有
联立方程有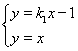 ,得
,得![]() ,
,
设直线![]() :
:![]() ,同理
,同理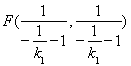 ,
,
因为![]() ,所以
,所以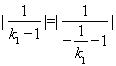 ,
,
①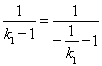 ,
,![]() 无实数解;
无实数解;
②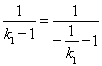 ,
,![]() ,
,![]() ,解得
,解得![]() ,
,
综上可得,直线![]() 的斜率为
的斜率为![]() .
.
18.解:(1)设![]() ,由题,
,由题,![]() 中,
中,![]() ,
,![]()
![]() ,
,
所以![]() ,在
,在![]() 中,
中,![]() ,
,![]()
![]() ,
,
由正弦定理得![]() ,
,
即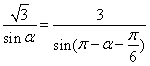 ,所以
,所以![]()
![]() ,
,
则![]()
![]()
![]() ,所以
,所以![]() ,
,
因为![]() 为锐角,所以
为锐角,所以![]() ,所以
,所以![]() ,得
,得![]() ;
;
(2)设![]() ,在
,在![]() 中,
中,![]() ,
,![]()
![]() ,
,
由正弦定理得![]() ,即
,即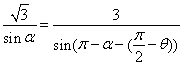 ,
,
所以![]()
![]()
![]()
![]() ,
,
从而![]()
![]() ,其中
,其中![]() ,
,![]() ,
,
所以![]() ,
,
记![]() ,
,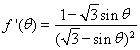 ,
,![]() ;
;
令![]() ,
,![]() ,存在唯一
,存在唯一![]() 使得
使得![]() ,
,
当![]() 时
时![]() ,
,![]() 单调增,当
单调增,当![]() 时
时![]() ,
,![]() 单调减,
单调减,
所以当![]() 时,
时,![]() 最大,即
最大,即![]() 最大,
最大,
又![]() 为锐角,从而
为锐角,从而![]() 最大,此时
最大,此时![]() .
.
答:观赏效果达到最佳时,![]() 的正弦值为
的正弦值为![]() .
.
19.解:(1)函数![]() 的定义域为
的定义域为![]() .当
.当![]() ,
,![]() ,
,![]() ,
,
∵![]() 恒成立,∴
恒成立,∴![]() 恒成立,即
恒成立,即![]() .
.
令![]() ,则
,则![]()
![]()
![]() ,
,
令![]() ,得
,得![]() ,∴
,∴![]() 在
在![]() 上单调递增,
上单调递增,
令![]() ,得
,得![]() ,∴
,∴![]() 在
在![]() 上单调递减,
上单调递减,
∴当![]() 时,
时,![]() .
.
∴![]() .
.
(2)①当![]() 时,
时,![]() ,
,![]() .
.
由题意,![]() 对
对![]() 恒成立,
恒成立,
∴![]() ,∴
,∴![]() ,即实数
,即实数![]() 的值为
的值为![]() .
.
②函数![]() 的定义域为
的定义域为![]() .
.
当![]() ,
,![]() ,
,![]() 时,
时,![]() .
.
![]() ,令
,令![]() ,得
,得![]() .
.
|
|
|
|
| - |
| + |
|
| 极小值 |
|
∴当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() .
.
对于![]() ,当
,当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,当
,当![]() 时,
时,
![]() .
.
∴当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() .
.
故函数![]() 的值域为
的值域为![]() .
.
20.解:(1)由![]()
![]() 得
得![]() ,两式作差得
,两式作差得![]() ,即
,即![]()
![]() .
.
![]() ,
,![]() ,所以
,所以![]()
![]() ,
,![]() ,则
,则![]()
![]() ,所以数列
,所以数列![]() 是首项为
是首项为![]() 公比为
公比为![]() 的等比数列,
的等比数列,
所以![]()
![]() ;
;
(2)由题意![]() ,即
,即![]() ,
,
所以![]() ,其中
,其中![]() ,
,![]() ,
,
所以![]() ,
,![]() ,
,
![]() ,所以
,所以![]() ,
,![]() ,
,![]() ;
;
(3)由![]()
![]()
![]() 得,
得,
![]()
![]()
![]() ,
,
![]()
![]()
![]() ,
,
![]()
![]() ,
,
所以![]()
![]() ,即
,即![]() ,
,
所以![]()
![]() ,
,
又因为![]() ,得
,得![]() ,所以
,所以![]()
![]() ,
,
从而![]()
![]()
![]() ,
,![]() ,
,
当![]() 时
时![]() ;当
;当![]() 时
时![]() ;当
;当![]() 时
时![]() ;
;
下面证明:对任意正整数![]() 都有
都有![]() ,
,
![]()
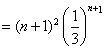
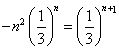
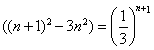
![]() ,
,
当![]() 时,
时,![]()
![]() ,即
,即![]() ,
,
所以当![]() 时,
时,![]() 递减,所以对任意正整数
递减,所以对任意正整数![]() 都有
都有![]() ;
;
综上可得,满足等式![]() 的正整数
的正整数![]() 的值为
的值为![]() 和
和![]() .
.
2017-2018学年度苏锡常镇四市高三教学情况调研(一)
数学Ⅱ(附加题)参考答案
21.【选做题】
A. 选修4-1:几何证明选讲
证明:(1)连接![]() ,
,![]() .因为
.因为![]() 是圆
是圆![]() 的直径,所以
的直径,所以![]() ,
,![]() .
.
因为![]() 是圆
是圆![]() 的切线,所以
的切线,所以![]() ,
,
又因为![]() ,所以
,所以![]() ,
,
于是![]() ,得到
,得到![]() ,
,
所以![]() ,从而
,从而![]() .
.
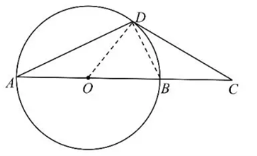
(2)解:由![]() 及
及![]() 得到
得到![]() ,
,![]() .由切割线定理,
.由切割线定理,![]() ,所以
,所以![]() .
.
B. 选修4-2:矩阵与变换
解:(1)![]() ;
;
(2)由![]() ,解得
,解得![]()
![]() ,又因为
,又因为![]() ,所以
,所以![]() ,
,![]() .
.
C. 选修4-4:坐标系与参数方程
解:在![]() 中,令
中,令![]() ,得
,得![]() ,
,
所以圆![]() 的圆心的极坐标为
的圆心的极坐标为![]() .
.
因为圆![]() 的半径
的半径![]()
![]() ,
,
于是圆![]() 过极点,所以圆的极坐标方程为
过极点,所以圆的极坐标方程为![]() .
.
D. 选修4-5:不等式选讲
证明:因为![]() ,
,![]() 都是正数,
都是正数,
所以![]() ,
,![]() ,
,
![]() ,又因为
,又因为![]() ,
,
所以![]() .
.
【必做题】
22.解:(1)以![]() 为原点,
为原点,![]() ,
,![]() ,
,![]() 为坐标轴,建立如图所示空间直角坐标系;设
为坐标轴,建立如图所示空间直角坐标系;设![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ;
;
所以![]() ,
,![]() ,
,![]() ,
,
设平面![]() 的法向量
的法向量![]() ,则
,则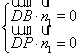 ,
,
即![]() ,解得
,解得![]() ,所以平面
,所以平面![]() 的一个法向量
的一个法向量![]() ,
,
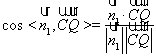
![]()
![]() ,
,
则![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.
(2)由(1)知平面![]() 的一个法向量为
的一个法向量为![]() ,设
,设![]() ,则
,则![]() ,
,![]()
![]()
![]() ,
,![]() ,设平面
,设平面![]() 的法向量
的法向量![]() ,则
,则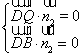 ,即
,即![]() ,解得
,解得![]() ,所以平面
,所以平面![]() 的一个法向量
的一个法向量![]() ,
,
由题意得![]()
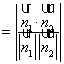
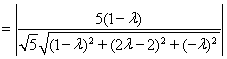 ,
,
所以![]() ,即
,即![]() ,
,
因为![]() ,所以
,所以![]() ,则
,则![]() .
.
23. 解:(1)![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
(2)![]() ,
,
理由如下:
对![]() 的元素的一个错位排列(
的元素的一个错位排列(![]() ,
,![]() ,…,
,…,![]() ),若
),若![]() ,分以下两类:
,分以下两类:
若![]() ,这种排列是
,这种排列是![]() 个元素的错位排列,共有
个元素的错位排列,共有![]() 个;
个;
若![]() ,这种错位排列就是将
,这种错位排列就是将![]() ,
,![]() ,…,
,…,![]() ,
,![]() ,…,
,…,![]() 排列到第
排列到第![]() 到第
到第![]() 个位置上,
个位置上,![]() 不在第
不在第![]() 个位置,其他元素也不在原先的位置,这种排列相当于
个位置,其他元素也不在原先的位置,这种排列相当于![]() 个元素的错位排列,共有
个元素的错位排列,共有![]() 个;
个;
根据![]() 的不同的取值,由加法原理得到
的不同的取值,由加法原理得到![]() ;
;
(3)根据(2)的递推关系及(1)的结论,![]() 均为自然数;
均为自然数;
当![]() ,且
,且![]() 为奇数时,
为奇数时,![]() 为偶数,从而
为偶数,从而![]() 为偶数,
为偶数,
又![]() 也是偶数,
也是偶数,
故对任意正奇数![]() ,有
,有![]() 均为偶数.
均为偶数.
下面用数学归纳法证明![]() (其中
(其中![]() )为奇数.
)为奇数.
当![]() 时,
时,![]() 为奇数;
为奇数;
假设当![]() 时,结论成立,即
时,结论成立,即![]() 是奇数,则当
是奇数,则当![]() 时,
时,![]() ,注意到
,注意到![]() 为偶数,又
为偶数,又![]() 是奇数,所以
是奇数,所以![]() 为奇数,又
为奇数,又![]() 为奇数,所以
为奇数,所以![]() ,即结论对
,即结论对![]() 也成立;
也成立;
根据前面所述,对任意![]() ,都有
,都有![]() 为奇数.
为奇数.
版权所有:南京市江宁高级中学 Copyright © 1999-2017 ALL Rights Reserved
信息发布:校务办公室 技术支持:信息中心 储老师